Тестирование онлайн
Арксинус, арккосинус, арктангенс, арккотангенс
Арксинус
Если есть выражение sinx=a, то x=arcsina. То есть арксинусом числа а называется такое число x , что его синус равен а.
Ограничения: 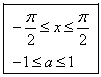


Арккосинус
Если есть выражение cosx=a, то x=arccosa. То есть арккосинусом числа а называется такое число x , что его косинус равен а.
Ограничения: 


Арктангенс
Если есть выражение tgx=a, то x=arctga. То есть арктангенсом числа а называется такое число x , что его тангенс равен а.
Ограничения: 


Арккотангенс
Если есть выражение сtgx=a, то x=arсctga. То есть арккотангенсом числа а называется такое число x , что его котангенс равен а.
Ограничения: 
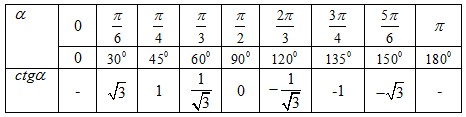
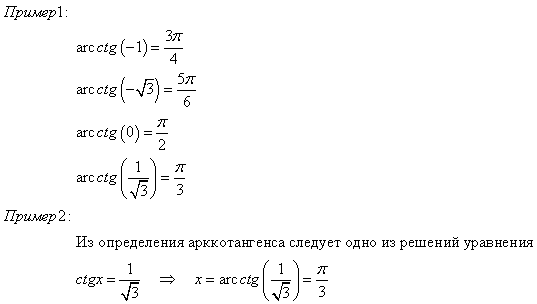
Не табличное значение "аркфункций" можно найти пользуясь калькулятором. Для того, чтобы понять почему у функций именно такие ограничения, необходимо изучить их графики.
Решение уравнения sinx=a
Общее решение уравнения



Частные случаи
 |  |
 |  |
 |  |
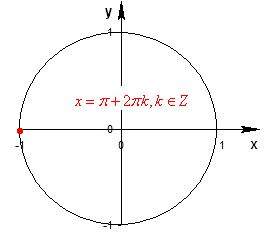
Решение уравнения cosx=a
Общее решение уравнения


Частные случаи
 |  |
 |  |
 |  |
Решение уравнения tgx=a, ctgx=a
Общее решение уравнения

Частные случаи для tgx=a
 |  |  |
Частные случаи для ctgx=a
 |  |  |
Методы решения тригонометрических уравнений
Метод подстановки. Метод используют, если в уравнение входят тригонометрические функции одного и того же аргумента.
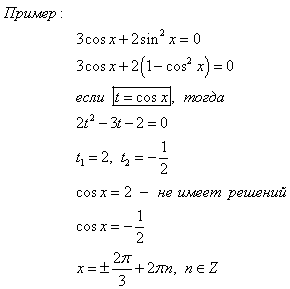
Решение однородных тригонометрических уравнений. Однородными называются уравнения вида:

Если  , то однородным уравнениям не удовлетворяют те значения x, при котором
, то однородным уравнениям не удовлетворяют те значения x, при котором  . Поэтому, разделив обе части каждого уравнения соответственно на
. Поэтому, разделив обе части каждого уравнения соответственно на  , не потеряем корней.
, не потеряем корней.

Метод разложения на множители при решении тригонометрических уравнений.

Использование формул универсальной подстановки.

Решений уравнений вида asinx+bcosx=c. Такие уравнения могут быть решены:
1) сведением к однородному

2) с помощью универсальной подстановки
3) с помощью формулы 
Метод введения дополнительного аргумента.

Метод оценки при решении тригонометрических уравнений.

