Тестирование онлайн

Признаки параллельности прямых

Определение. Две прямые на плоскости называются параллельными, если они не пересекаются (не имеют ни одной общей точки).

Прямая называется секущей по отношению к прямым, если она пересекает их в двух точках.

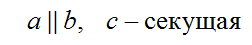
При пересечении прямых секущей образуется восемь углов. Некоторые пары этих углов имеют специальные названия.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰, то прямые параллельны.

Справедливы обратные теоремы:

Теорема 1. Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Теорема 2. Если две параллельные прямые пересечены секущей, то соответственные углы равны.

Теорема 3. Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180⁰.

Аксиома параллельных прямых. Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Следствие 1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.

Следствие 2. Если две прямые параллельны третьей прямой, то они параллельны.