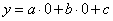Математика
Тестирование онлайн
Определение. График
Квадратичной (квадратной) функцией называется функция вида
где a, b, с - числа.
Графиком квадратичной функции является парабола.
Парабола имеет вершину, ось, проведенная через вершину и параллельная оси Оу, делит параболу на две симметричные части. Вершиной параболы называется точка
Если коэффициент а>0, то ветви параболы направлены вверх, если a<0, то ветви параболы направлены вниз.
Свойства квадратичной функции y=x2
1) Областью определения функции 
является множество всех действительных чисел, т.е. 
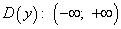
2) Множеством значений функции является промежуток 
3) Значение функции y=0 является наименьшим, а наибольшего значения функция не имеет.
4) Функция является четной, график симметричен относительно оси Оу.
5) Функция непериодическая.
6)Парабола имеет с осями координат единственную общую точку (0;0) - начало координат.
7) Значение аргумента x=0 является нулем функции.
8) На промежутке 
функция убывающая, а на промежутке 
- возрастающая.
9) Функция принимает положительные значения на множестве 
, т.е. все точки параболы, кроме начала координат.
Преобразование параболы
Функция y=x2 - частный случай квадратичной функции.
Квадратичную функцию 
всегда можно привести у виду 
, а затем построить параболу с помощью ее геометрических преобразований.
Для построения параболы необходимо:
1) Найти координаты вершины
2) Построить ось симметрии, проанализировать куда направлены ветви параболы
3) Найти точки пересечения параболы с осью Ox (нули), если они есть, решив уравнение 
4) Найти точку пересечения с осью Оу, решив уравнение 